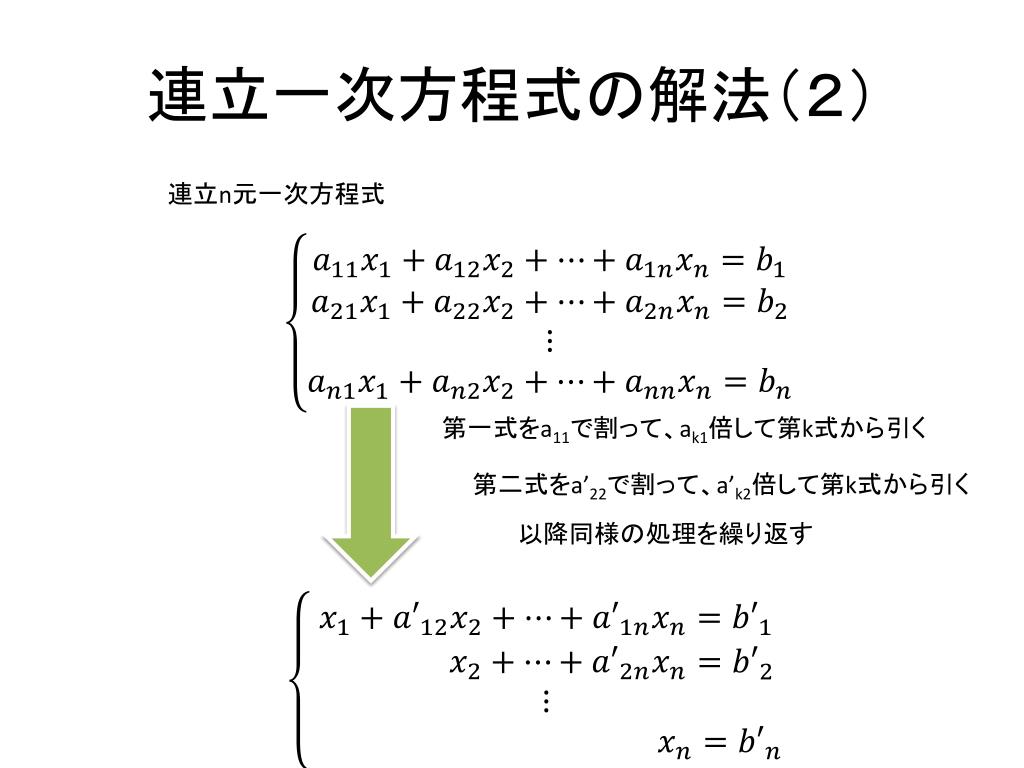
2元1次方程式 名前 ① 2元1次方程式 の解をすべて求めなさい。 ただし、解は自然数である。 ② 2元1次方程式 の解をすべて求めなさい。 ただし、解は自然数である。 ③ ① 、② をもとにして、連立方程式 の解を求めなさい。 ① ( , )が連立方程式 の解である2元連立1 次方程式の簡便解法 未知数が の1次方程式2本からなる連立方程式: の解法について考えます。 1 普通に解くと... 普通に解いてみます。なお, とします。これは, のどれもが0でないということです。0ではないので,これらの文字を①4元1次方程式 { a 11 x 1 a 12 x 2 a 13 x 3 a 14 x 4 = b 1 a 21 x 1 a 22 x 2 a 23 x 3 a 24 x 4 = b 2 a 31 x 1 a 32 x 2 a 33 x 3 a 34 x 4 = b 3 a 41 x 1 a 42 x 2 a 43 x 3 a 44 x 4 = b 4
2
2元1次方程式 とは
2元1次方程式 とは-1 まとめとして,一般の2元連立1次方程式の解の分類を記述しておく. 11 12 1 21 22 2 (1) (2) ax a y b ax a y b ìïï = í ïïî = 直線 直線 (41) が与えられたとき,解は次表によって分類される.ただし,a12¢は行基本変形を行った最中学校では連立2元1次方程式は本格的に扱うが、連立3元1次方程式は「研究」で出てくるだけで、取り扱わないだろう。 以前は、連立3元1次方程式もとりあつかっていたが・・・・・・。 教師用のいわゆる赤本には、留意事項中学校では、連立2元1次方程式までしか学習していない。 ここでは、求める2次関数をy=a・x^2bx+cとおいて、a,b,cに関する連立3元1次方程式を




連立方程式の2つの解き方 代入法 加減法 数学fun
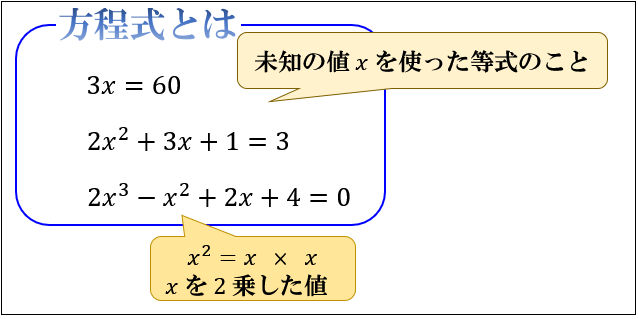
1 2元連立1 次方程式の解法 x とy を未知数とする次の連立方程式 を行列を使って次のように表すことができる。 (1) 式(1)のa ,b, c, d を要素とした行列の行列式(determinant)をD とすると, である。2つの2元1次方程式を1組と考えたものを連立方程式または 連立2元1次方程式といい,右のように表す。 連立方程式で,2つの方程式を同時に成り立たせるx,yの値の組を,連立方程式の解といい,解を 求めることを,連立方程式を解くという。 二次方程式 っていう単元だ。 因数分解や平方根をガンガンつかうから、中3数学の総まとめってかんじ。 けっこう、手強いよ。 今日は、この単元の基礎をおさえるために、 2次方程式とはいったいなにものか?? を勉強していこう。 二次方程式とはずばり
二元連立方程式 関数電卓が手元にないとき、面倒事を押し付けれて非常に助かります。 sqrt (値)のように使用します。 連立方程式の問題の答え合わせ。 とても便利でしたが途中の式や、分数表示ができない点が残念でした。 宿題の答え合わせに使いました。 途中式を表示していただけると分からなかった所を解きなおしできたりするのでお願いします。 使い 連立方程式の文章題は解き方の本質ではない! どこで利用するかが大事 数検1級合格対策 資格 → 漢検1級 ・ 数検1級(高校で合格) ・英検1級→ G11 学歴 → 東京大学大学院 (12年3月) 趣味 → 筋トレ でフィジーク体型目指してます。 発信 →その他1次式 ⇒ 次数の最大値が1の文字式。例えば「x1」 1次方程式 ⇒ 等式となる1次式。例えば「x1=0」 方程式の詳細は下記をご覧ください。 方程式とは?1分でわかる意味、移項、1次方程式の解き方と計算問題、分数の関係 1次式と2次式の違い
2元1次不定方程式の整数解 a x b y = c a, b は互いに素とする。 解を1つ見つける。 その解を ( x, y) = ( x 0, y 0) とすると元の不定方程式は a ( x − x 0) b ( y − y 0) = 0 となる。 t ∈ Z として x − x 0 = b t, y − y 0 = − a t が一般解となる。 a と b は互いに素な2次方程式とは? では、この単元で扱う2次方程式とは何か?というと、"1元2次"方程式になります。 元が1つなので元の部分は基本省略されて、2次方程式と呼ばれています。 では、例えば、どのようなものが2次方程式と呼ばれるかというと、 \(x^{2}6x8=0\) や 12已知关于x的方程3a﹣x= 3的解为2,则代数式a2﹣2a1的值是 1 考点一元一次方程的解 分析先把x=2代入方程求出a的值,再把a的值代入代数式进行计算即可 解答解∵关于x的方程3a﹣x= 3的解为2,




スプリックス 二元一次方程式の解 3 Youtube



連立方程式とは 連立方程式とその解 教遊者
目次 1 1次不定方程式の単元で学習すること 2 1次不定方程式について 3 1次不定方程式の解き方と解の表し方 31 1次不定方程式の解き方 32 1次不定方程式の一般解を求めてみよう 4 1次不定方程式を扱った問題を解いてみよう 41 問(1)の解答・解説; こんにちはもちもちの実です! 今回は、2元1次不定方程式の整数解の求め方について解説していきます。 それでは本編へどうぞ! 1 整数解の存在条件 前提として、a,bは整数とします。このとき、 a,bは互いに素⇔axby=1を満たすx,yの整数解は存在 が成り立つ。 2元1次2 16年10月22日 18年3月16日 2元1次不定方程式の整数解の理論の問題です。 一般的な解の求め方、解の存在条件の問題です。 まずはユークリッドの互除法を用いて解く理論から。 ややこしく見えますが、前問でやったことを文字に置き換えてやって



1次方程式と2元連立1次方程式
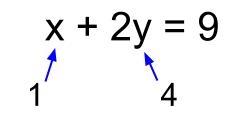



中学数学 2元1次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su
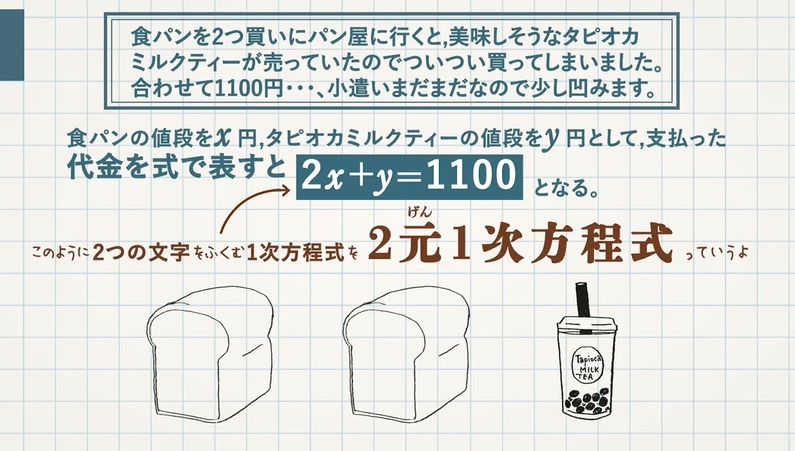
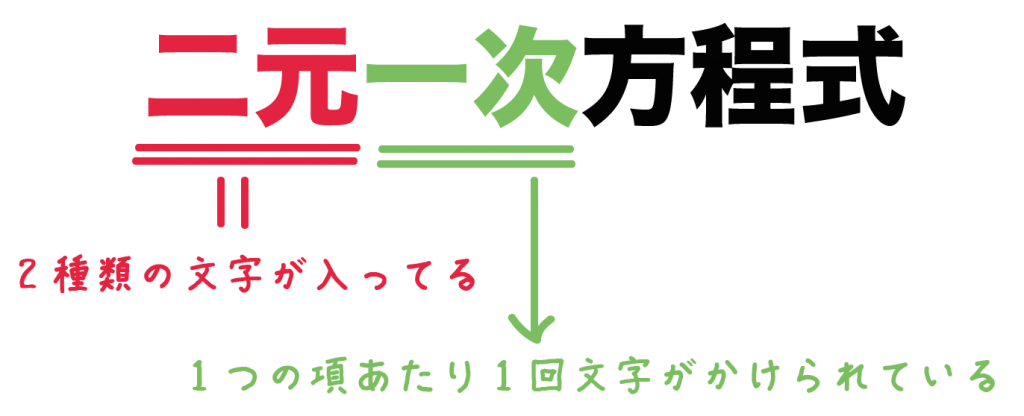
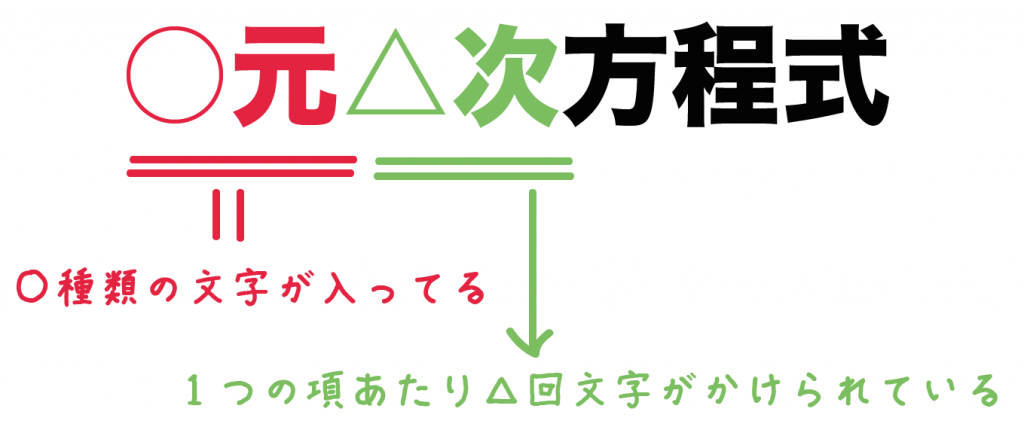
只含有一个 未知数 (一元),并且未知数项的最高 次数 是2(二次)的 整式方程 叫做一元二次方程 。 一元二次方程经过整理都可化成一般形式ax²bxc=0(a≠0)。 其中ax²叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项 。2元1次方程式と呼ばれる「 2つの変数 (文字) 」と「 最大次数が1 」の式で表されます。 連立方程式の解き方は大きく2つあります。Yの係数を同じにしてから2元1次方程式をことわってください。 2元1次方程式(axby=p,cxby=qの法則) 高精度計算サイト ゲストさん




中学2年数学 1次関数 2元1次方程式とグラフ 確認問題4 あんのん塾



Ppt 連立一次方程式の解法 1 Powerpoint Presentation Free Download Id
二元一次方程的解法加减消元法 (1)概念:当方程中两个方程的某一未知数的系数相等或 互为相反数 时,把这两个方程的两边相加或相减来消去这个未知数,从而将二元一次方程化为一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法定理(連立2元1次方程式の解の公式) 連立方程式 ‰ axby = p cxdy = q はad¡bc 6= 0 ならば解けて,解は x = dp¡bq ad¡bc;X, y を未知数とする 連立2元1次方程式 (simultaneous linear equations with two unknowns) { a 1 x b 1 y = c 1 a 2 x b 2 y = c 2 の解を求めるために、未知数 x, y の一方を消去します。 まずは、 x を求めるために y を消去します。




12 1 X Y T 5 3 2 1 2x 3y Lihat Cara Penyelesaian Di Qanda




高校数学 文字係数の2元連立1次方程式 受験の月
このページのテーマは「1元2次方程式1 基本」です。 小学校3年生向けの無料数学PDFプリント集です。 計算問題,文章題を中心としてランダムの数値を使って大量作成しました。Y = aq ¡pc ad¡bc 注意 連立方程式を解く方法には充分慣れていることでしょうから,この解の公式は覚 える必要はありません5。この公式の良さは,一般の場合にも同じような形の 一元二次方程怎么解,一元一次方程呢,二元方程,2次方程,最好举个例子我是个六年级刚毕业的学生,报了名,在学校里老师必需让买的作业,只有数学很难,全都没学过,都是初中的,急 作业帮 —— 一元二次,就是值1个未知数,然后是两次方,比如x^2=5,这时候需要开根号




第4回講義 基礎数学
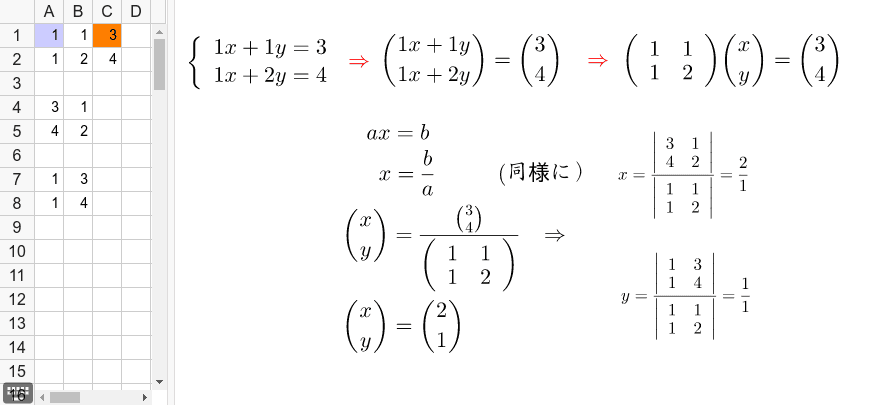



二元一次連立方程式 Geogebra
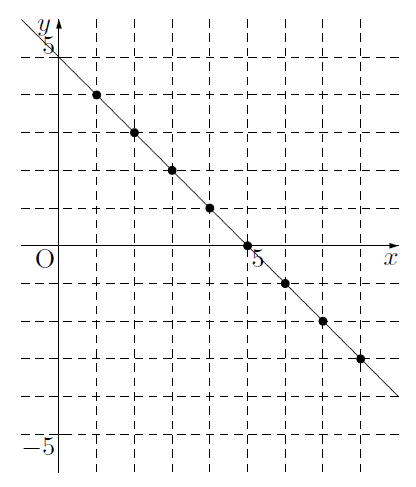
連立方程式の解が1つに決まる理由 どうして式が2つあると解が1つに決まるのでしょうか? 一言で言えば、 「同一平面上の2直線は、『重なっている場合』と『平行の場合』を除けば、 必ずどこかで交わる 」からです。 そして2元1次方程式の解は直線でしたね2元1次方程式とは x2y = 9 x 2 y = 9 このように、 2 2 種類の文字の項がある 1 1 次式を、方程式と見た場合 2 2 元 1 1 次方程式といいます。 ※関数とみれば 1 1 次関数(次の章で学びます)です。 あまり言葉にこだわる必要はありません。 等式の変形をすることで x2y = 9 x 2 y = 9 2y = −x 9 2 y = − x 9 y =− y = − 1 2 1 2 x x 9 2 9 2二次方程式1 ===≪2次方程式の解≫=== 解説 → の応用として, すなわち のような2次方程式も解くことができます. ※この変形方法を使えば,別の頁で扱っている「因数分解による解き方」では解けないような問題でも解くことができます.この変形




2元1次方程式とグラフの書き方 中2数学 Youtube




Begincasesxy52xy6endcas Descubre Como Resolverlo En Qanda
2元1次不定方程式の解き方、2通り 2x+3y=1(x、yは整数)① を解きましょう。 特に難しいというのでもなく、教科書にも載っている普通の問題です。 まず特殊解を見つけます。 つまり①を満たすx、yの具体例を見つけます。 カンで分かるでしょう。 x=ー1、y=1でよいですね。 するともちろん




要点 連立3元1次方程式の解き方 Youtube



2元1次連立方程式から2次の行列式へ




1次関数と2元1次方程式の違い Youtube



Service Zkai Co Jp Jr Koritsu Pdf Vm2hy Pdf




2元1次方程式 無料で使える中学学習プリント




連立3元1次方程式 身勝手な主張



第1章 連立方程式
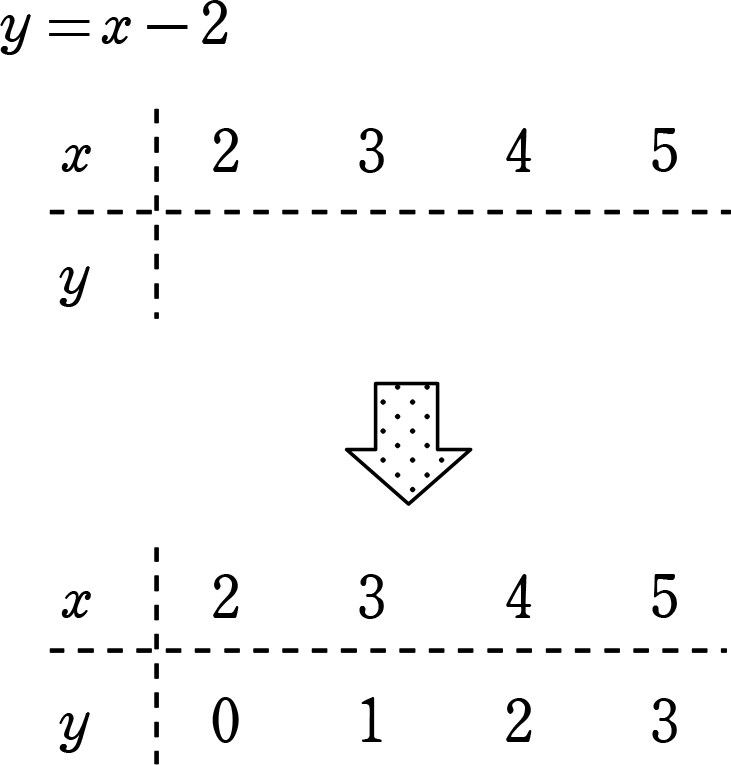



中学数学 連立方程式 二元一次




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
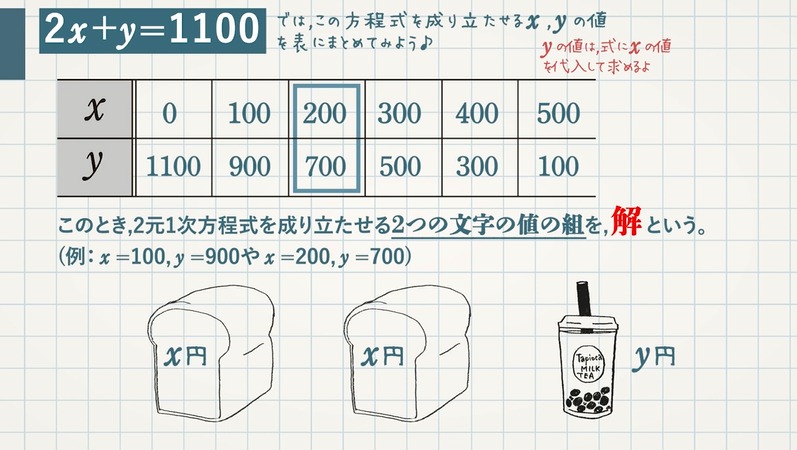



連立方程式とは 連立方程式とその解 教遊者




中2数学 連立方程式 1 1 2元1次方程式 Youtube



2




1 2 1 2x3y3 Descubre Como Resolverlo En Qanda



3
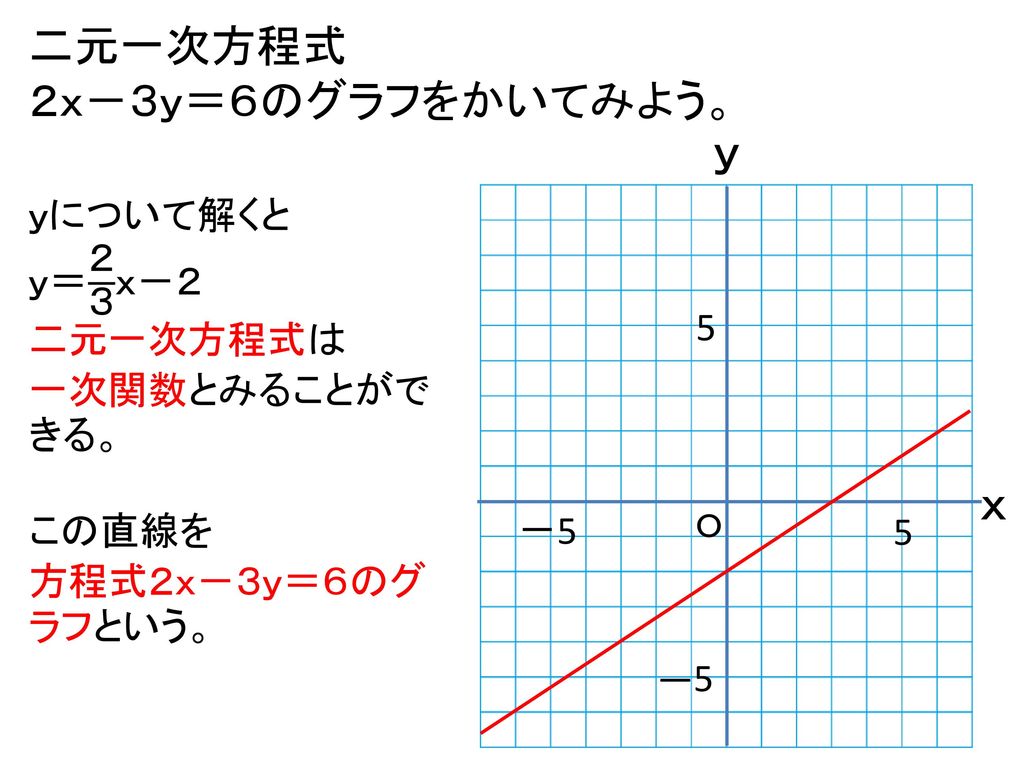



一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download




連立方程式とその解 まなびの学園




三元1次方程式の計算法 Youtube




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張




121 3x 2 212 1 21 Y 214 Descubre Como Resolverlo En Qanda
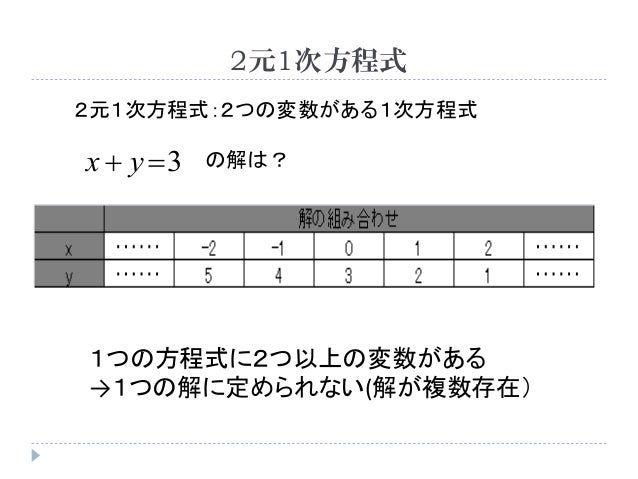



連立方程式 連立方程式の意味と一般的な解法




食塩水の濃度に関する連立2元1次方程式の応用問題 中学校2年生の数学より 身勝手な主張



第1章 連立方程式




連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri



2元1次方程式のグラフ まなびの学園




連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張




写真の1答えを教えてください できれば 解説も 中2 連立方程式 Clear




中学数学 中学2年 Vol 017 連立方程式の解き方 連立方程式とその解 二元一次方程式 Youtube



1




数学の力を付けるヒントがある 齊藤数学教室 算数オリンピックから大学数学入門




連立方程式の2つの解き方 代入法 加減法 数学fun



二元一次方程式とか一元一次方程式とかの一元とか二元ってどういう意味があるので Yahoo 知恵袋



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく



2




高校数学 2元2次連立方程式3パターン 受験の月




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




第4回講義 基礎数学




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ



二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




中学数学 一次方程式




スプリックス 二元一次方程式の解 3 Youtube



2次方程式の解き方 補足 二元二次連立方程式 難 数学の解説と練習問題



2元1次方程式 Of Tomorrow Land




中2 二元一次方程式 解の求め方 日本語版 Youtube




ม 3 โน ตของ 中2 連立方程式とグラフ 完全版 ช น Junior Clear



第1章 連立方程式




行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download
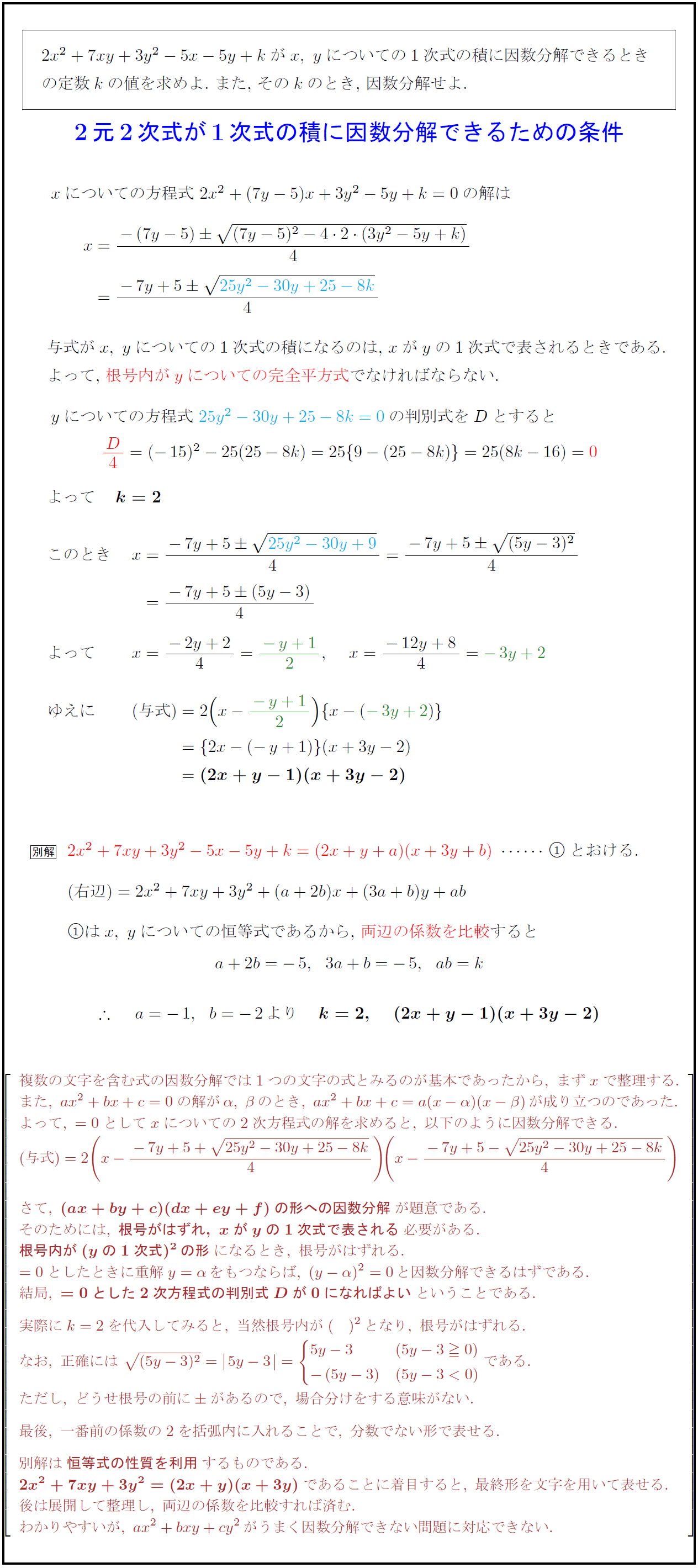



高校数学 2元2次式が1次式の積に因数分解できるための条件 受験の月



Http Www Nyushi Sugaku Com Tyu2 T2 3 Y 05 Pdf




連立方程式の解の判別式と行列式 行列式 1 大学生 専門学校生 社会人 数学のノート Clear



1
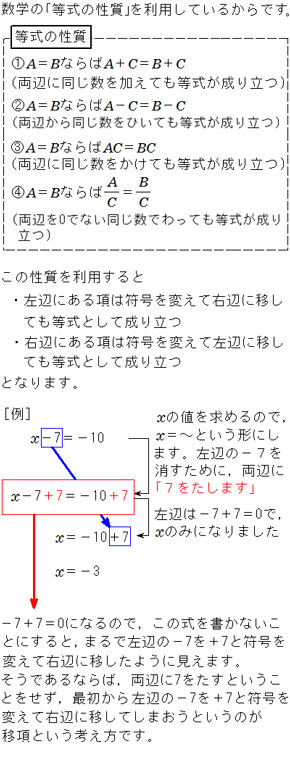



1次方程式 なぜ移項するとき符号がかわるのか 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張




二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題




メンバー限定 中2 2元1次方程式と連立方程式 Campfireコミュニティ




連立3元1次方程式 まなびの学園




I221 Descubre Como Resolverlo En Qanda



Numpyで2元1次方程式の解を求める 偏った言語信者の垂れ流し




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




2元一次方程式のグラフの問題です 答えはx軸に平行な直線の式 関数で ある Clear
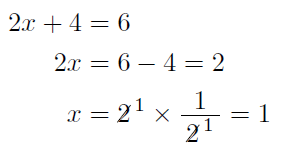



2元1次方程式 まなびの学園




1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト
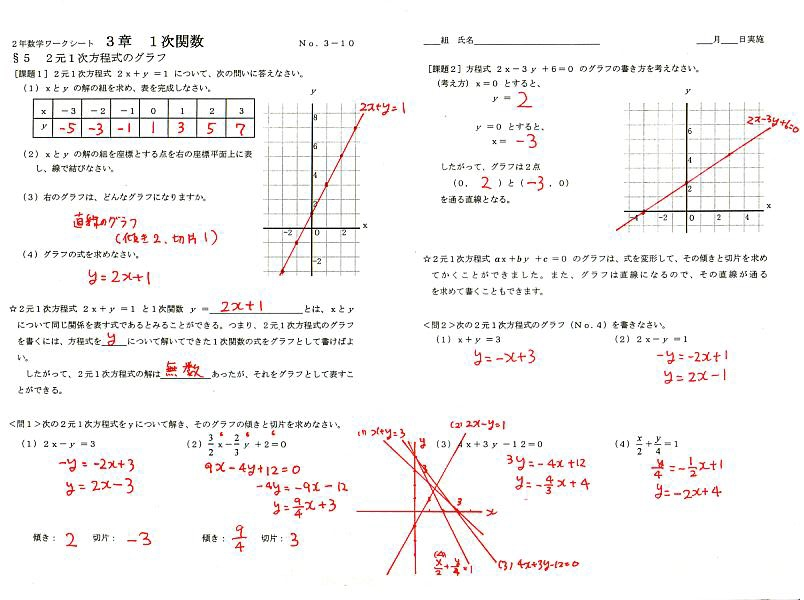



5 2元1次方程式のグラフ Mathweather4067のblog



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典




2次方程式の文章問題 自然数や整数を求める問題 バカでもわかる 中学数学



第1章 連立方程式




中学数学1年 1次方程式の利用 整数 受験の月




中2数学 二元一次方程式 証明 中学生 数学のノート Clear
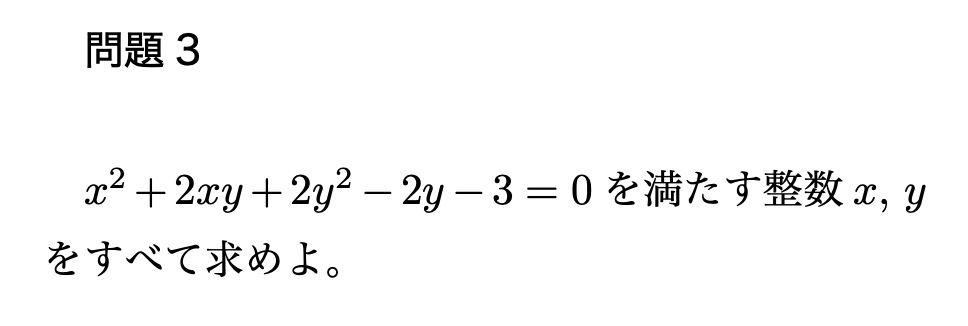



不定方程式の解き方とは 全4パターンを東大医学部生がわかりやすく解説 東大医学部生の相談室




二元一次方程式にする前の掛け算はなぜこのようなかけ方法を行ってるのですか Clear




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




数学 中2 35 二元一次方程式のグラフを書く Youtube



中3 二次方程式の文章題 中学数学の方程式 中間 期末テスト 高校入試対策




連立二元一次方程式をクラメールの公式で解く 身勝手な主張




最も好ましい 3 連立 方程式 シモネタ



2元1次不定方程式x 29y ーの整数解として現れるxの値のうち Yahoo 知恵袋



Studydoctor2元1次方程式とグラフの書き方 中2数学 Studydoctor



1




中2数学 2元1次方程式グラフです Clear




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張



第1章 連立方程式



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく



Http Www Juen Ac Jp G Katei Nunokawa Function 2 2 5 Pdf




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




高校数学 3元連立1次方程式 一般型と循環型 受験の月




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




例題 連立3元1次方程式の解き方 Youtube




2元1次不定方程式 2 x 29y 1 の整数解を一組求めよ Clear


